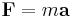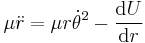Centrifugal force

Not to be confused with Centripetal force.
Classical mechanics
\mathbf{F} = m \mathbf{a}
History of classical mechanics · Timeline of classical mechanics
Fundamental concepts
Space · Time · Velocity · Speed · Mass · Acceleration · Gravity · Force · Impulse · Torque / Moment / Couple · Momentum · Angular momentum · Inertia · Moment of inertia · Reference frame · Energy · Kinetic energy · Potential energy · Mechanical work · Virtual work · D'Alembert's principle

Centrifugal force (from Latin centrum, meaning "center", and fugere, meaning "to flee") represents the effects of inertia that arise in connection with rotation and which are experienced as an outward force away from the center of rotation. In Newtonian mechanics, the term centrifugal force is used to refer to one of two distinct concepts: an inertial force (also called a "fictitious" force) observed in a non-inertial reference frame, and a reaction force corresponding to a centripetal force.

The term is also sometimes used in Lagrangian mechanics to describe certain terms in the generalized force that depend on the choice of generalized coordinates.

The concept of centrifugal force is applied in rotating devices such as centrifuges, centrifugal pumps, centrifugal governors, centrifugal clutches, etc., as well as in centrifugal railways, planetary orbits, banked curves, etc. These devices and situations can be analyzed either in terms of the fictitious force in the rotating coordinate system of the motion relative to a center, or in terms of the centripetal and reactive centrifugal forces seen from a non-rotating frame of reference; these different centrifugal forces are not equal in general.

Contents

History of conceptions of centrifugal and centripetal forces

Main article: History of centrifugal and centripetal forces

The conception of centrifugal force has evolved since the time of Huygens, Newton, Leibniz, and Hooke who expressed early conceptions of it. The modern conception as a fictitious force or pseudo force due to a rotating reference frame as described above evolved in the eighteenth and nineteenth centuries.

Centrifugal force has also played a role in debates in classical mechanics about detection of absolute motion. Newton suggested two arguments to answer the question of whether absolute rotation can be detected: the rotating bucket argument, and the rotating spheres argument.[1] According to Newton, in each scenario the effects attributed to the centrifugal force would only be observed in the frame where the objects are stationary if that frame itself were rotating with respect to absolute space. Nearly two centuries later, Mach's principle was proposed, where, instead of absolute rotation, a physical law, which relates the motion of the distant stars to the local inertial frame force, gives rise to the centrifugal force and other inertia effects. Today's view is based upon the idea of an inertial frame of reference, which privileges observers for which the laws of physics take on their simplest form, and in particular, do not need to use centrifugal forces in their equations of motion in order to describe motions correctly.

The analogy between centrifugal force (sometimes used to create artificial gravity) and gravitational forces led to the equivalence principle of general relativity.[2][3]

Fictitious centrifugal force

Main article: Centrifugal force (rotating reference frame)

Centrifugal force is often confused with centripetal force. Centrifugal force is most commonly introduced as a force associated with describing motion in a non-inertial reference frame, and referred to as a fictitious or inertial force (a description that must be understood as a technical usage of these words that means only that the force is not present in a stationary or inertial frame).[4][5]

There are three contexts in which the concept of the fictitious force arises when describing motion using classical mechanics:[6]

In the first context, the motion is described relative to a rotating reference frame about a fixed axis at the origin of the coordinate system. For observations made in the rotating frame, all objects appear to be under the influence of a radially outward force that is proportional to the distance from the axis of rotation and to the square of the rate of rotation (angular velocity) of the frame.

The second context is similar, and describes the motion using an accelerated local reference frame attached to a moving body, for example, the frame of passengers in a car as it rounds a corner.[6] In this case, rotation is again involved, this time about the center of curvature of the path of the moving body. In both these contexts, the centrifugal force is zero when the rate of rotation of the reference frame is zero, independent of the motions of objects in the frame.[7]

The third context is the most general, and subsumes the first two, as well as stationary curved coordinates (e.g., polar coordinates),[8][9][10][11] and more generally any system of abstract coordinates as in the Lagrangian formulation of mechanics.

If objects are seen as moving from a rotating frame, this movement results in another fictitious force, the Coriolis force; and if the rate of rotation of the frame is changing, a third fictitious force, the Euler force is experienced. Together, these three fictitious forces allow for the creation of correct equations of motion in a rotating reference frame.[7]

Reactive centrifugal force

Main article: Reactive centrifugal force

A reactive centrifugal force is the reaction force to a centripetal force. A mass undergoing curved motion, such as circular motion, constantly accelerates toward the axis of rotation. This centripetal acceleration is provided by a centripetal force, which is exerted on the mass by some other object. In accordance with Newton's Third Law of Motion, the mass exerts an equal and opposite force on the object. This is the reactive centrifugal force. It is directed away from the center of rotation, and is exerted by the rotating mass on the object that originates the centripetal acceleration.[12][13][14]

This conception of centrifugal force is very different from the fictitious force. As they both are given the same name, they may be easily conflated. Whereas the 'fictitious force' acts on the body moving in a circular path, the 'reactive force' is exerted by the body moving in a circular path onto some other object. The former is useful in analyzing the motion of the body in a rotating reference frame; the latter is useful for finding forces on other objects, in an inertial frame.

This reaction force is sometimes described as a centrifugal inertial reaction,[15][16] that is, a force that is centrifugally directed, which is a reactive force equal and opposite to the centripetal force that is curving the path of the mass.

The concept of the reactive centrifugal force is sometimes used in mechanics and engineering. It is sometimes referred to as just centrifugal force rather than as reactive centrifugal force.[17][18]

Fictitious vs. reactive force

The table below compares various facets of the "fictitious force" and "reactive force" concepts of centrifugal force

Fictitious centrifugal force Reactive centrifugal force
Reference
frame		 Non-inertial frames Any
Exerted
  by		 Acts as if emanating
from the rotation axis,
but no real source		 Bodies moving in
curved paths
Exerted
  upon		 All bodies, moving or not;
if moving, Coriolis force
also is present		 The object(s) causing
the curved motion, not upon
the body in curved motion
Direction Away from rotation axis,
regardless of path of body		 Opposite to the
centripetal force
causing curved path
Analysis Kinetic:
included as force in
Newton's laws of motion		 Kinematic:
related to
centripetal force

Use of the term in Lagrangian mechanics

See also: Lagrangian and Mechanics of planar particle motion

Lagrangian mechanics formulates mechanics in terms of generalized coordinates 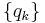\{q_k\}, which can be as simple as the usual polar coordinates 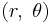(r,\ \theta) or a much more extensive list of variables.[19][20] Within this formulation the motion is described in terms of generalized forces, using in place of Newton's laws the Euler–Lagrange equations. Among the generalized forces, those involving the square of the time derivatives 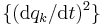\{(\mathrm{d}q_k/\mathrm{d}t)^2\} are sometimes called centrifugal forces.[21][22][23][24]

The Lagrangian approach to polar coordinates that treats 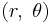(r,\ \theta) as generalized coordinates, 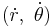(\dot{r},\ \dot{\theta}) as generalized velocities and 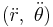(\ddot{r},\ \ddot{\theta}) as generalized accelerations, is outlined in another article, and found in many sources.[25][26][27] For the particular case of single-body motion found using the generalized coordinates 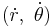(\dot{r},\ \dot{\theta}) in a central force, the Euler–Lagrange equations are the same equations found using Newton's second law in a co-rotating frame. For example, the radial equation is:

\mu\ddot{r} = \mu r\dot\theta^2 - \frac{\mathrm{d}U}{\mathrm{d}r}

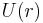where U(r) is the central force potential and μ is the mass of the object. The left side is a "generalized force" and the first term on the right is the "generalized centrifugal force". However, the left side is not comparable to a Newtonian force, as it does not contain the complete acceleration, and likewise, therefore, the terms on the right-hand side are "generalized forces" and cannot be interpreted as Newtonian forces.[28]

The Lagrangian centrifugal force is derived without explicit use of a rotating frame of reference,[29] but in the case of motion in a central potential the result is the same as the fictitious centrifugal force derived in a co-rotating frame.[6] The Lagrangian use of "centrifugal force" in other, more general cases, however, has only a limited connection to the Newtonian definition.

References

  1. ^ An English translation is found at Sir Isaac Newton (1934). Philosophiae naturalis principia mathematica (Andrew Motte translation of 1729, revised by Florian Cajori ed.). University of California Press. pp. 10-12. http://books.google.com/books?id=ySYULc7VEwsC&pg=PA10. 
  2. ^ Barbour, Julian B. and Herbert Pfister (1995). Mach's principle: from Newton's bucket to quantum gravity. Birkhäuser. ISBN 0817638237, p. 69.
  3. ^ Eriksson, Ingrid V. (2008). Science education in the 21st century. Nova Books. ISBN 1600219519, p. 194.
  4. ^ Takwale, R. G. and P. S. Puranik (1980). Introduction to classical mechanics. Tata McGraw-Hill. ISBN 9780070966178, p. 248.
  5. ^ Jacobson, Mark Zachary (1980). Fundamentals of atmospheric modeling. Cambridge: University Press. ISBN 9780521637176, p. 80.
  6. ^ a b c See p. 5 in Donato Bini, Paolo Carini, Robert T Jantzen (1997). "The intrinsic derivative and centrifugal forces in general relativity: I. Theoretical foundations". International Journal of Modern Physics D 6 (1). http://www34.homepage.villanova.edu/robert.jantzen/research/articles/idcf1.pdf. . The companion paper is Donato Bini, Paolo Carini, Robert T Jantzen (1997). "The intrinsic derivative and centrifugal forces in general relativity: II. Applications to circular orbits in some stationary axisymmetric spacetimes". International Journal of Modern Physics D 6 (1). http://www34.homepage.villanova.edu/robert.jantzen/research/articles/idcf2.pdf. 
  7. ^ a b Fetter, Alexander L. and John Dirk Walecka (2003). Theoretical Mechanics of Particles and Continua (Reprint of McGraw-Hill 1980 ed.). Courier Dover Publications. ISBN 0486432610, pp. 38–39.
  8. ^ "Classical Dynamics of Particles and Systems", Marion and Thornton, Brooks Cole; 5 edition 2003.
  9. ^ "Methods of Applied Mathematics" By Francis B. Hildebrand, 1992, Dover, p 156.
  10. ^ "Statistical Mechanics" By Donald Allan McQuarrie, 2000, University Science Books.
  11. ^ "Essential Mathematical Methods for Physicists" By Hans-Jurgen Weber, George Brown Arfken, Academic Press, 2004, p 843.
  12. ^ Mook, Delo E. & Thomas Vargish (1987). Inside relativity. Princeton NJ: Princeton University Press. ISBN 0691025207, p. 47.
  13. ^ Signell, Peter (2002). "Acceleration and force in circular motion" Physnet. Michigan State University, "Acceleration and force in circular motion", §5b, p. 7.
  14. ^ Mohanty, A. K. (2004). Fluid Mechanics. PHI Learning Pvt. Ltd. ISBN 8120308948, p. 121.
  15. ^ Roche, John (September 2001). "Introducing motion in a circle". Physics Education 43 (5), pp. 399-405, "Introducing motion in a circle". Retrieved 2009-05-07.
  16. ^ Lloyd William Taylor (1959). Physics, the pioneer science. 1. Dover Publications. p. 173. http://books.google.com/?id=fp84AAAAIAAJ&q=%22centrifugal+inertial+reaction%22&dq=%22centrifugal+inertial+reaction%22. 
  17. ^ Edward Albert Bowser (1920). An elementary treatise on analytic mechanics: with numerous examples (25th ed.). D. Van Nostrand Company. p. 357. http://books.google.com/?id=mE4GAQAAIAAJ&pg=PA357. 
  18. ^ Joseph A. Angelo (2007). Robotics: a reference guide to the new technology. Greenwood Press. p. 267. ISBN 1573563374. http://books.google.com/?id=73kNFV4sDx8C&pg=PA267. 
  19. ^ For an introduction, see for example Cornelius Lanczos (1986). The variational principles of mechanics (Reprint of 1970 University of Toronto ed.). Dover. p. 1. ISBN 0486650677. http://books.google.com/?id=ZWoYYr8wk2IC&pg=PR4&dq=isbn=0486650677#PPR21,M1. 
  20. ^ For a description of generalized coordinates, see Ahmed A. Shabana (2003). "Generalized coordinates and kinematic constraints". Dynamics of Multibody Systems (2 ed.). Cambridge University Press. p. 90 ff. ISBN 0521544114. http://books.google.com/?id=zxuG-l7J5rgC&printsec=frontcover#PPA90,M1. 
  21. ^ Christian Ott (2008). Cartesian Impedance Control of Redundant and Flexible-Joint Robots. Springer. p. 23. ISBN 3540692533. http://books.google.com/?id=wKQvUfwzqjAC&pg=PA23. 
  22. ^ Shuzhi S. Ge, Tong Heng Lee, Christopher John Harris (1998). Adaptive Neural Network Control of Robotic Manipulators. World Scientific. pp. 47–48. ISBN 981023452X. http://books.google.com/books?id=cdBENqlY_ucC&printsec=frontcover&dq=CHristoffel+centrifugal&lr=&as_brr=0#PPA47,M1. "In the above Euler–Lagrange equations, there are three types of terms. The first involves the second derivative of the generalized co-ordinates. The second is quadratic in 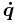\boldsymbol{\dot q} where the coefficients may depend on 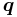\boldsymbol{q}. These are further classified into two types. Terms involving a product of the type 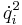{\dot q_i}^2 are called centrifugal forces while those involving a product of the type 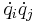\dot q_i \dot q_j for i ≠ j are called Coriolis forces. The third type is functions of 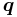\boldsymbol{q} only and are called gravitational forces." 
  23. ^ R. K. Mittal, I. J. Nagrath (2003). Robotics and Control. Tata McGraw-Hill. p. 202. ISBN 0070482934. http://books.google.com/?id=ZtwMEQzMVlMC&pg=PA202. 
  24. ^ T Yanao & K Takatsuka (2005). "Effects of an intrinsic metric of molecular internal space". In Mikito Toda, Tamiki Komatsuzaki, Stuart A. Rice, Tetsuro Konishi, R. Stephen Berry. Geometrical Structures Of Phase Space In Multi-dimensional Chaos: Applications to chemical reaction dynamics in complex systems. Wiley. p. 98. ISBN 0471711578. http://books.google.com/?id=2M4qIUTITI0C&pg=PA98. "As is evident from the first terms …, which are proportional to the square of 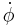\dot\phi, a kind of "centrifugal force" arises … We call this force "democratic centrifugal force". Of course, DCF is different from the ordinary centrifugal force, and it arises even in a system of zero angular momentum." 
  25. ^ John R Taylor (2005). Classical Mechanics. Sausalito, Calif.: Univ. Science Books. pp. 299 ff. ISBN 189138922X. http://books.google.com/?id=P1kCtNr-pJsC&pg=PA299. 
  26. ^ Francis Begnaud Hildebrand (1992). Methods of Applied Mathematics (Reprint of 1965 2nd ed.). Courier Dover Publications. p. 156. ISBN 0486670023. http://books.google.com/?id=17EZkWPz_eQC&pg=PA156&dq=absence+fictitious+force. 
  27. ^ V. B. Bhatia (1997). Classical Mechanics: With Introduction to Nonlinear Oscillations and Chaos. Alpha Science Int'l Ltd.. p. 82. ISBN 8173191050. http://books.google.com/?id=PmXYkwFGnX0C&pg=PA82. 
  28. ^ Henry M. Stommel and Dennis W. Moore (1989). An Introduction to the Coriolis Force. Columbia University Press. pp. 36–38. 
  29. ^ Edmond T Whittaker (1988). A treatise on the analytical dynamics of particles and rigid bodies (Reprint of 1917 2nd ed.). Cambridge University Press. pp. 40–41. ISBN 0521358833. http://books.google.com/?id=epH1hCB7N2MC&printsec=frontcover#PPA40,M1.